Pythonによる離散フーリエ変換
本記事では，周波数解析の方法の一つとして用いられている離散フーリエ変換（計算機上での演算では高速フーリエ変換）の実装方法について取り上げます．
勉強中なので足りない点があるかもしれませんが，ご了承ください．
ざっくりフーリエ変換とは
フーリエ変換とは無限長の連続信号（アナログ信号）があったときにこれを無限の周波数を持つ $sin$, $cos$ の重ね合わせで表現する方法で，時間軸を周波数軸に変換することができます．
変換する上ではどこかで区切らなければならないので無限長を扱うことは難しく，有限長の連続信号には周期的に同様の信号が現れているという仮定の下でフーリエ級数展開が使われます．
しかし，現実にはこれらの方法で信号を解析することはできません．コンピュータでアナログ信号を扱うことはできないからです．
そういうわけで，有限長の $N$ 個の周波数の $sin$, $cos$ の重ね合わせでデジタル信号を変換する手法として，離散フーリエ変換 (discrete Fourier transform, DFT) が用いられます．
また，実際に演算を行う際には高速フーリエ変換 (fast Fourier transform, FFT) を用います．計算量がデータ数が $N$ のとき $O(N^2)$ から $O(N\log_{2}N)$ に抑えられるので，文字通り高速化が期待できます．
フーリエ変換はデータの性質がわかるというだけでなく，ノイズの除去やデータの圧縮などにも応用されています．
離散フーリエ変換
離散フーリエ変換とは、複素関数 $f(x)$ を複素関数 $F(t)$ に写す写像であって、次の式で定義されるものを言う。
$$ F(t)=\sum_^{N-1} f(x)e^{-i \frac{2\pi tx}{N}} $$
ここで、$N$は任意の自然数、$e$ はネイピア数、$i$ は虚数単位 $i^{2}=-1$で、$\pi$ は円周率である。このとき、$x=0, \dots ,N-1$を標本点という。また、この変換を $\mathcal{F}_N$という記号で表し、
$$ F=\mathcal{F}_N(f) $$
のように略記することが多い。 この逆変換にあたる逆離散フーリエ変換（英語: inverse discrete Fourier transform、IDFT）は
$$ f(x)=\frac{1}{N} \sum_^{N-1} F(t)e^{i \frac{2\pi xt}{N}} $$
定義式は書籍によって異なっているようです．
エイリアシング
離散フーリエ変換では有限個の標本点から逆離散フーリエ変換で元の関数を写像できます．
$f(x)$ → $F(t)$ → $g(x)$ と変換したとき，標本点上では $f(x)=g(x)$ が成り立ちますが，それ以外の点でも成り立つとは限りません．同じ標本点を持つ関数が他にも存在し得るからです．
これがエイリアシングと呼ばれる問題です．ある標本点から元の関数を完全に復元するためには，サンプリング定理を満たす必要があります．
サンプリング定理
サンプリング定理とは，サンプリング周波数を解析する信号の周波数の２倍以上に設定しなければならないというものです．
しかし，周波数解析では元の信号の周波数を知りたいから解析するのであって，２倍といっても具体的な値を考えることはできません．
そのため，エイリアシングを解消する方法としては二つ考えられます．
- 十分大きいサンプリング周波数を設定する
- ローパスフィルタをかけてアンチエイリアスを行う
ローパスフィルタでは，ナイキスト周波数（サンプリング周波数 / 2）以上の高周波を取り除く処理をします．
サンプリング周波数 $f_S$ の設定で気をつけなければならないのは，離散フーリエ変換では標本数 $N$ のときに調べられる周波数の間隔は $\frac{f_S}{N}$ であるということです．
サンプリング周波数が大きければ大きいほど周波数の一単位も大きくなってしまうため，何が何でも大きい値を取ればよいというわけではありません．
Python による実装
上記の内容を踏まえ，FFT を実装します．
FFT では任意のデータ数の信号を扱うことができるようですが，最も効率的に計算できるのはデータ数が２の冪乗になっているときです．
Python パッケージでは numpy による実装と，scipy による実装がよく見られますが，今回は scipy を使います．
import matplotlib.pyplot as plt
import numpy as np
from scipy.fftpack import fft, fftfreq
# 標本数
N = 2**10
# サンプリング間隔 (= 1 / サンプリング周波数)
dt = 1e-2
t = np.arange(0, N * dt, dt)
# ナイキスト周波数
nyquist = 1 / dt / 2
# 振幅
A1, A2 = 3, 5
# 周波数
f1, f2 = 2, 7
y = A1 * np.sin(2 * np.pi * f1 * t) + A2 * np.sin(2 * np.pi * f2 * t)
# 周波数スケール
freq = fftfreq(N, dt)
F = fft(y)
# 正規化
F = F / (N / 2)
# ローパスフィルタ
F[(freq > nyquist)] = 0
fig = plt.figure(figsize=(9.6, 9.6))
# 信号データ
ax1 = fig.add_subplot(311)
ax1.plot(t, y)
ax1.set_xlim([0, 5])
ax1.set_xlabel('step')
ax1.set_ylabel('signal')
# 振幅スペクトル
ax2 = fig.add_subplot(312)
ax2.plot(freq[1:N//2], np.abs(F)[1:N//2])
ax2.set_xlabel('frequency [Hz]')
ax2.set_ylabel('Amplitude')
# パワースペクトル
ax3 = fig.add_subplot(313)
ax3.plot(freq[1:N//2], (F**2)[1:N//2])
ax3.set_xlabel('frequency [Hz]')
ax3.set_ylabel('Power')
plt.show()
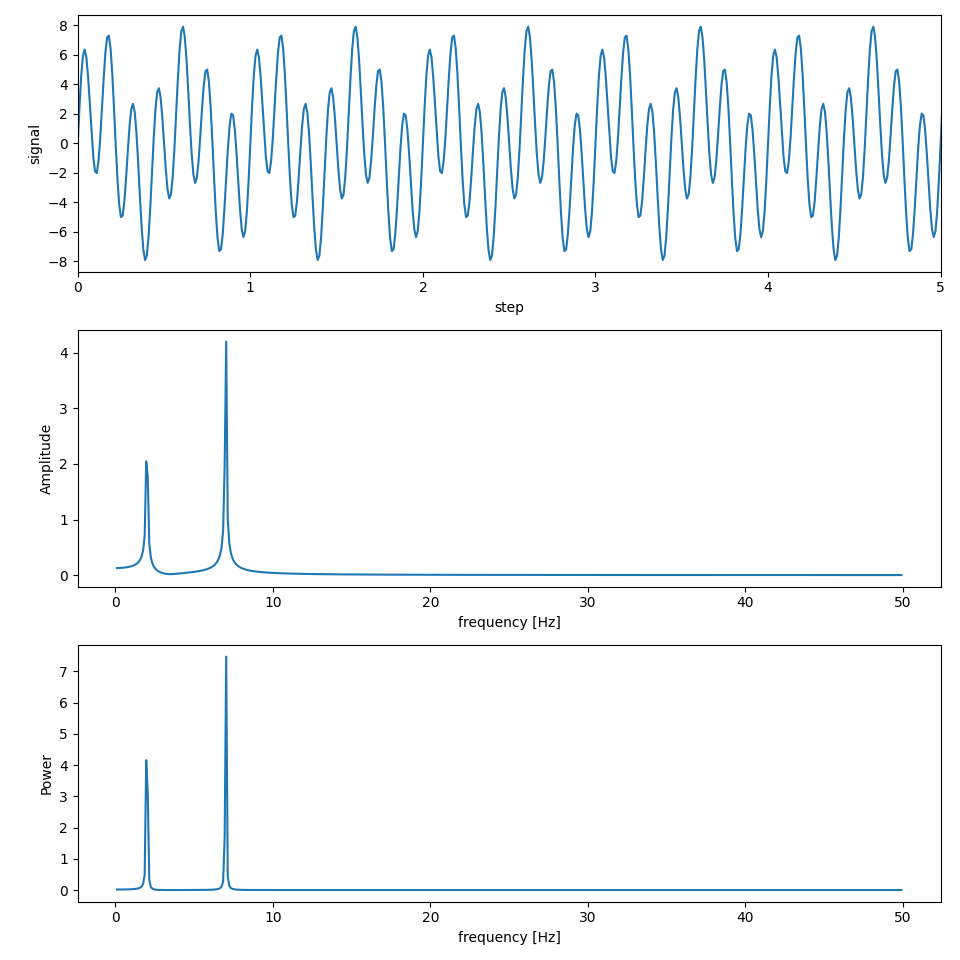
途中で正規化するのは，DFT して得られる結果と元の信号の振幅が対応していないからです．上記の定義式では DFT, IDFT の正規化係数が $1, \frac{1}{N}$ となっていることが確認できます．
また，交流成分については２倍するという処理を同時に行っていますが，これはエイリアシング現象によってナイキスト周波数を中心にデータが対象になっているため，値の大きさが二等分されているものを修正しています．
周波数は 2, 7 でしたが，この結果からどちらも解析できていることがわかりました．
ちなみに，DFT による写像の絶対値を振幅スペクトル，２乗をパワースペクトルと呼びます．
おまけ：短時間フーリエ変換
DFT, IDFT は音響・音声界隈などでもよく使われている手法です．
DFT を拡張した短時間フーリエ変換 (Short-time Fourier transform, STFT) が用いられます．
今回は詳細を省きますが，簡単に説明すると窓関数を用いて信号の連続性（というより周期性）を保とうとしながら一定の長さの信号のフーリエ変換を行っていく方法です．
この結果はいわゆる音響スペクトログラムとして得られます．
例えば，ある歌を思い浮かべると数分間から切り出したときにメロディーはそれぞれ異なっており，全体の特徴を一度に掴むのは難しそうです．
そのため，時間方向に情報を圧縮した DFT ではなく，一定時間ごとの周波数の強さを見ることができる STFT が向いているというわけです．
窓関数の必要性
一つの区間を取ってきて DFT することを繰り返すのが STFT ですが，単純に取ってきた信号をそのまま DFT するには問題があります．
そもそもフーリエ変換は周期性がある信号を入力とすることを仮定しており，テキトーな区間で抽出してきたデータを繰り返したときに始点と終点が連続にならないのでは，この仮定が崩れてしまいます．
しかし，信号の特徴が分かっていない状態で周期性を保つように区間を決めるのは難しいことです．
そのため，窓関数を使って周期的に変化するような信号として入力することが必要とされています．
今回は以上です．何かご指摘があれば Twitter 等へお願いします．